“เมทริกซ์” เป็นหัวข้อหนึ่งในวิชาคณิตศาสตร์ที่น่าสนใจและน่าจะเป็นอีกเรื่องหนึ่งที่น่าปวดหัวสำหรับ
น้อง ๆ หลายคน บทความนี้พี่ TUTOR VIP จึงจะมาสรุปแบบกระชับ เพื่อให้น้อง ๆ เข้าใจเมทริกซ์ได้ง่ายยิ่งขึ้น ตามไปดูกันเลย!
เลือกอ่านเนื้อหาที่ต้องการ
เมทริกซ์ คืออะไร?
“เมทริกซ์” คือ การเรียงจำนวนจริงให้เป็นแถว โดยแต่ละแถวมีจำนวนๆ เท่าๆ กัน ภายใน ( ) หรือ [ ] แต่ละจำนวนในเมทริกซ์ จะเรียกว่า “สมาชิกของเมทริกซ์” เรียกแต่ละช่องในแนวนอนว่า “แถว” เรียกแต่ละช่องในแนวตั้งว่า “หลัก” และเรียกแถว X หลักว่า “มิติ” หรือ “ขนาด” เช่น เมทริกซ์ A มีขนาด m n จะหมายถึง เมทริกซ์ A มีจำนวน m แถว และมี n หลัก
ตัวอย่างของเมทริกซ์
กำหนดเมทริกซ์ A ดังนี้

เมทริกซ์ A เป็นเมทริกซ์ที่มี 3 แถว และ 4 หลัก จะได้ว่า เมทริกซ์ A มีมิติ 3 4 โดยที่
- สมาชิกแถวที่ 1 หลักที่ 1 คือ 2
- สมาชิกแถวที่ 1 หลักที่ 2 คือ -1
- สมาชิกแถวที่ 1 หลักที่ 3 คือ 2
- สมาชิกแถวที่ 1 หลักที่ 4 คือ 2
- สมาชิกแถวที่ 2 หลักที่ 1 คือ 2
- สมาชิกแถวที่ 2 หลักที่ 2 คือ 3
- สมาชิกแถวที่ 2 หลักที่ 3 คือ 0
- สมาชิกแถวที่ 2 หลักที่ 4 คือ 5
- สมาชิกแถวที่ 3 หลักที่ 1 คือ 2
- สมาชิกแถวที่ 3 หลักที่ 2 คือ 2
- สมาชิกแถวที่ 3 หลักที่ 3 คือ -1
- สมาชิกแถวที่ 3 หลักที่ 4 คือ 3
นิยามของเมทริกซ์
- การเรียกชื่อ เมทริกซ์ โดยปกติแล้วจะใช้ตัวอักษรภาษาอังกฤษตัวใหญ่แทนชื่อเมทริกซ์
- สมาชิกของเมทริกซ์ที่เรียงกันอยู่ตามแนวนอน เรียกว่าสมาชิกที่อยู่ในแถว (row) ของเมทริกซ์
- สมาชิกของเมทริกซ์ที่เรียงกันอยู่ตามแนวตั้ง เรียกว่าสมาชิกที่อยู่ในหลัก (column) ของเมทริกซ์
- การบอกตำแหน่งของสมาชิกในเมทริกซ์ จะบอกโดยการระบุ แถวที่… และหลักที่… ตามลำดับ
การเขียนเมทริกซ์ในรูปทั่วไป
การเขียนสัญลักษณ์แทนเมทริกซ์ในรูปทั่วไปจะใช้ A = [ a_{ij} ] m x n
โดยที่ a_{ij} จะใช้แทนสมาชิกของ a ในหลักที่ i หลักที่ j
ตัวอย่างของการเขียนเมทริกซ์ในรูปทั่วไป
- A =

ดังนั้น A เป็นเมทริกซ์ที่มี 1 แถว 4 หลัก ดังนั้น A มีมิติ 1x4 หรือเป็นเมทริกซ์ 1x4
มี a_{11} = 2 a_{12} = 5 a_{13} = -3 a_{14} = 1
- B =

ดังนั้น B เป็นเมทริกซ์ที่มี 2 แถว 3 หลัก ดังนั้น B มีมิติ 23 หรือเป็นเมทริกซ์ 23
มี a_{11} = 1 a_{12} = 1 a_{13} = -3 , a_{21} = 0 a_{22} = -2 a_{23} = 2
ประเภทของเมทริกซ์ที่ควรรู้
ประเภทของเมทริกซ์ที่พบได้บ่อย และควรรู้มีดังนี้
1.เมทริกซ์จัตุรัส (square matrix)
คือ เมทริกซ์ที่มีจำนวนแถว และหลักเท่ากัน หรือเป็นเมทริกซ์ที่มีมิติ n x n
เช่น A = 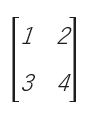
จะเห็นได้ว่า A เป็นเมทริกซ์ที่มี 2 แถว และ2 หลักเท่ากัน จึงเป็นเมทริกซ์จตุรัส
2. เมทริกซ์ศูนย์ (zero matrix)
คือ เมทริกซ์ที่สมาชิกทุกตัวเป็น 0 ทั้งหมด ใชัสัญลักษณ์ ![]() = 0_{m x n}
= 0_{m x n}
เช่น 0_{2x3} = 
3. เมทริกซ์สามเหลี่ยมบน (Upper triangular matrix)
คือ เมทริกซ์จัตุรัสที่สมาชิกของเมทริกซ์ทุกตัวที่อยู่ใต้เส้นทแยงมุมหลักมีค่าเท่ากับ 0 ส่วนตำแหน่งที่เหลือมีค่าเท่าไรก็ได้
เช่น 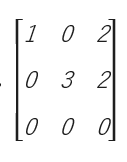
4. เมทริกซ์สามเหลี่ยมล่าง (Lower triangular matrix)
คือ เมทริกซ์จัตุรัสที่มีสมาชิกทุกตัวซึ่งอยู่เหนือเส้นทแยงมุมหลักมีค่าเท่ากับ 0 ส่วนสมาชิกที่อยู่บนเส้นทแยงมุมหลักหรืออยู่ใต้เส้นทแยงมุมหลักจะมีค่าเท่าไรก็ได้
เช่น 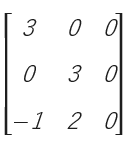
5. เมทริกซ์เฉียง (Diagonal matrix)
คือ เมทริกซ์จัตุรัส ที่มีสมาชิกที่ไม่อยู่บนเส้นทแยงมุมหลัก โดยทุกตัวมีค่า เป็น 0 ทั้งหมด
เช่น 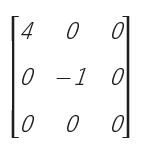
6. เมทริกซ์สเกลาร์ (Scalar matrix)
คือ เมทริกซ์จัตุรัสที่มีสมาชิกทุกตัวบนเส้นทแยงมุมหลักมีค่าเท่ากัน ส่วนสมาชิกอื่นที่เหลือมีค่าเป็น 0 ทั้งหมด
เช่น 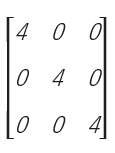
7. เมทริกซ์เอกลักษณ์ (Identity matrix)
คือ เมทริกซ์จัตุรัสที่มีสมาชิกทุกตัวบนเส้นทแยงมุมหลักมีค่าเป็น 1 ส่วนสมาชิกอื่นที่เหลือมีค่าเป็น 0 ทั้งหมด เราจะใช้ l_n แทนเมทริกซ์เอกลักษณ์ที่มีมิติ n x n
เช่น l_3 = 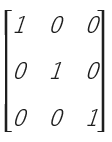
8. เมทริกซ์แบบแถว (Row matrix)
คือ เมทริกซ์ที่มีกี่หลักก็ได้ แต่ต้องมีเพียง 1 แถวเท่านั้น
เช่น 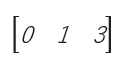
9. เมทริกซ์แบบหลัก(Column matrix)
คือ เมทริกซ์ที่มีกี่แถวก็ได้ แต่ต้องมีเพียง 1 หลักเท่านั้น
เช่น A = 
เป็นอย่างไรกันบ้างเอ่ย ดูแล้วอาจรู้สึกว่าเยอะและยากแต่หากทบทวนและฝึกทำโจทย์อย่างสม่ำเสมอแล้ว พี่เชื่อว่าน้อง ๆ จะต้องทำได้แน่นอน และหวังว่าบทความนี้จะทำให้น้อง ๆ เข้าใจและสนุกกับเมทริกซ์กันมากขึ้นนะ
ส่วนใครที่กำลังมองหาที่ติวคณิตศาสตร์ หรือมีข้อสงสัยเพิ่มเติมก็มาปรึกษาพี่ TUTOR VIP ได้นะ พี่ ๆ ยินดีให้คำปรึกษาเสมอ
บทความต่อไป TUTOR VIP จะมาแนะนำอะไรอีกนั้น ฝากติดตามกันด้วยนะ
ด้วยความร่วมมือของ TUTOR-VIP X Clearnote Thailand





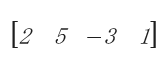
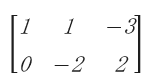




บทความล่าสุด
วิทยาศาสตร์
พลังงานไฟฟ้า เกิดขึ้นได้อย่างไร ปัจจุบันนี้มีวิธีผลิตกี่แบบ มาหาคำตอบกัน
วิทยาศาสตร์
ไฟฟ้ากระแสตรง(DC) และกระแสสลับ(AC) แตกต่างกันอย่างไร? มาไขคำตอบกัน
สังคมและประวัติศาสตร์
พระราชประวัติ และ พระราชกรณียกิจ สมเด็จพระนางเจ้าสิริกิติ์ ฯ