พื้นฐานทฤษฎีบทพีทาโกรัสที่ควรรู้

    “ทฤษฎีบทพีทาโกรัส” เป็นบทเรียนพื้นฐานที่น้อง ๆ จะได้เรียนกันในวิชาคณิตศาสตร์ตั้ง

แต่ระดับชั้น ม.ต้น เชื่อว่าหลายคนแค่ได้ยินชื่อนี้ก็อาจจะเบือนหน้าหนีกันแล้ว

     บทความนี้ พี่TUTOR VIP จึงได้สรุป “ทฤษฎีบทพีทาโกรัส” ให้กระชับที่สุด เพื่อให้น้อง ๆ เข้าใจกันได้ง่ายยิ่งขึ้น  ตามไปดูกันเลย

เลือกอ่านเนื้อหาที่ต้องการ

• ทฤษฎีบทพีทาโกรัส คืออะไร?
• ตัวอย่างการใช้ทฤษฎีบทพีทาโกรัส
• ตัวอย่างโจทย์ทฤษฎีพีทาโกรัส

ทฤษฎีบทพีทาโกรัส คืออะไร?

    ทฤษฎีบทพีทาโกรัส คือ ทฤษฎีความสัมพันธ์ระหว่างด้านทั้งสามของสามเหลี่ยมมุมฉาก สามเหลี่ยมที่มีมุมใดมุมหนึ่งตั้งฉาก 90 องศา เป็นทฤษฎีที่คิดค้นโดยพีทาโกรัส นักคณิตศาสตร์ชาวกรีก  ซึ่งกล่าวถึงทฤษฎีนี้ไว้ว่า

“ในสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น”

    ทฤษฎีนี้ ถือเป็นพื้นฐานสำคัญในการนำไปปรับใช้และคำนวณในโจทย์ประยุกต์ต่าง ๆ ทางคณิตศาสตร์ โดยเฉพาะเรื่องตรีโกณมิติ

ตัวอย่างการใช้ทฤษฎีบทพีทาโกรัส

    เพื่อให้น้อง ๆ เห็นภาพของทฤษฎีบทพีทาโกรัสกันมากขึ้น โดยพิจารณารูปสามเหลี่ยมมุมฉาก ดังนี้

ทฤษฎีบทพีทาโกรัส สามารถเขียนแทนสมการได้เป็น  a² + b² = c²  โดย 

• ด้าน ab เป็น ด้านตรงข้ามมุมฉาก อยู่ตรงข้ามกับมุม c แทนด้วยความยาว c
• ด้าน ac เป็น ด้านประชิดมุมฉาก อยู่ตรงข้ามกับมุม b แทนด้วยความยาว b
• ด้าน bc เป็น ด้านประชิดมุมฉาก อยู่ตรงข้ามกับมุม a แทนด้วยความยาว a

     ซึ่งหากทราบความยาวของมุม 2 ด้าน จะสามารถหาความยาวของด้านที่ 3 ได้ทันที โดยใช้ทฤษฎีบทพีทาโกรัสในการคำนวณ เขียนเป็นสมการได้ดังนี้

• กรณีที่ทราบความยาวของด้านประชิดมุมฉาก a และ b จะสามารถหาค่าของ c ได้ ดังนี้

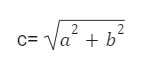
• กรณีที่ทราบความยาวของด้านตรงข้ามมุมฉาก c และด้านประชิดมุมฉากด้านใดด้านหนึ่ง a หรือ b จะสามารถหาค่าของด้านที่เหลือได้ ดังนี้

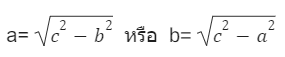
ตัวอย่างโจทย์ทฤษฎีบทพีทาโกรัส

    หลังจากได้ทำความรู้จักหลักการของทฤษฎีบทพีทาโกรัสแล้ว ลองมาดูโจทย์จริง ๆ กันบ้างดีกว่า 

จงหาความยาวด้านที่เหลือของสามเหลี่ยมมุมฉากต่อไปนี้

วิธีทำ

       จากภาพ a=4 , b=3 จงหาค่าของ c

       จะได้ว่า     c²      =       4² +  3²

                       c²      =      (4 x 4) + (3 x 3)

                       c²      =      16 + 9

                       c²      =      25

                       c²      =      5²

ดังนั้น              c        =      5

ตอบ   c ยาว 5 หน่วย

    เป็นอย่างไรกันบ้าง พอดูแล้วก็ไม่ยากอย่างที่คิดใช่ไหมเอ่ย?  หวังว่าบทความนี้จะทำให้น้อง ๆ เข้าใจและสนุกกับคณิตศาสตร์กันมากขึ้นนะ

    ส่วนใครที่กำลังมองหาที่ติวคณิตศาสตร์ หรือมีข้อสงสัยเพิ่มเติมก็มาปรึกษาพี่ TUTOR VIP ได้นะ พี่ ๆ ยินดีให้คำปรึกษาเสมอ

   บทความต่อไป TUTOR VIP จะมาแนะนำอะไรอีกนั้น ฝากติดตามกันด้วยนะ

ด้วยความร่วมมือของ TUTOR-VIP X Clearnote Thailand