“จำนวนเชิงซ้อน” เป็นอีกบทเรียนที่น่าจะเข้าใจยากสำหรับน้อง ๆ หลายคน แต่ก็เป็นบทเรียนที่สำคัญและไม่ควรละเลย บทความนี้พี่ ๆ TUTOR VIP จึงจะมาสรุปพื้นฐานของจำนวนเชิงซ้อนแบบย่อยง่าย เพื่อให้น้อง ๆ เข้าใจเรื่องนี้กันได้มากขึ้น จะมีเนื้อหาอะไรบ้างตามไปดูกันเลย
เลือกอ่านเนื้อหาที่ต้องการ
จำนวนเชิงซ้อน คืออะไร?
“จำนวนเชิงซ้อน” (Complex Number) คือ จำนวนที่เขียนในได้ในรูป ![]() เมื่อ a และ b เป็นจำนวนจริง และ
เมื่อ a และ b เป็นจำนวนจริง และ ![]() หรือ
หรือ ![]()
จำนวนเชิงซ้อนเกิดขึ้นจากความพยายามของนักคณิตศาสตร์ในการแก้สมการ ![]() ซึ่งเป็นจำนวนจริงไม่สามารถหาจํานวนจริงใด ๆ ที่แทนใน x แล้วทําให้สมการเป็นจริงได้
ซึ่งเป็นจำนวนจริงไม่สามารถหาจํานวนจริงใด ๆ ที่แทนใน x แล้วทําให้สมการเป็นจริงได้
นิยามของจำนวนเชิงซ้อน
- เรียก a ว่า ส่วนจริง (Real Part) ของ z เขียนแทนด้วย Re(Z)
- เรียก b ว่า ส่วนจินตภาพ (Imaginary Part) ของ z เขียนแทนด้วย Im(Z)
- ถ้า Im(Z)=0 แล้ว z เป็นจำนวนจริง ถ้า Re(Z)=0 และ Im(Z) ไม่เท่ากับ 0 แล้ว z จะเป็นจำนวนจินตภาพแท้
ตัวอย่างเช่น
จะได้ว่า -2 คือส่วนจริง และ 1 คือส่วนจินตภาพ หรือเขียนได้ว่า (-2,1)
จะได้ว่า 3 คือส่วนจริง และ 2 คือส่วนจินตภาพ หรือสามารถเขียนได้ว่า 3,2
1.การเท่ากันของจำนวนเชิงซ้อน
เมื่อกำหนดให้ (a,b) และ (c,d) เป็นจํานวนเชิงซ้อนสองจํานวน
(a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
2.การบวกของจำนวนเชิงซ้อน
เมื่อกำหนดให้ (a,b) และ (c,d) เป็นจํานวนเชิงซ้อนสองจํานวน
(a, b) + (c, d) = (a + c, b + d)
การบวกจำนวนเชิงซ้อน คือ การนำส่วนจริงตัวหน้าและส่วนจินตภาพตัวหลังของทั้งสองจำนวนมาบวกกัน
ตัวอย่าง
จงหาผลบวกของจำนวนเชิงซ้อน (8, -4) และ (2, 10)
วิธีทำ
(8, -4) + (2, 10) = (8+2), (-4+10)
= (10, 6)
3.การลบของจำนวนเชิงซ้อน
บทนิยาม
(a , b)- (c , d) = (a , b) + (-c , -d)
ใช้หลักการคล้ายกับการบวกจำนวนเชิงซ้อน คือการนำส่วนจริงมาลบกับส่วนจริง
และนำส่วนจินตภาพมาลบกับส่วนจินตภาพ
ตัวอย่าง
จงหาผลลบของจำนวนเชิงซ้อน (-3, 11)- (-7 , -19)
วิธีทำ
(-3,11) – (-7,-19) = (-3+7,11+19)
= (4, 30)
4.การคูณของจำนวนเชิงซ้อน
ใช้สมบัติการแจกแจงคล้ายกับการคูณพหุนาม คือตัวหน้าคูณตัวหน้า ตัวหน้าคูณตัวหลัง ตัวหลังคูณตัวหน้า ตัวหลังคูณตัวหลัง
เมื่อกำหนดให้ (a,b) และ (c,d) เป็นจํานวนเชิงซ้อนสองจํานวน
(a, b)(c, d) = (ac – bd, ad + bc)
ตัวอย่าง
จงหาผลคูณของจำนวนเชิงซ้อน (8, -4) และ (2, 10)
วิธีทำ
(8, -4) (2, 10) = (8×2) – (-4×10), (8×10+(-4)x2)
= (56, 72)
5.การหารของจำนวนเชิงซ้อน
บทนิยาม
สำหรับจำนวนเชิงซ้อน z และ w ใด ๆ ซึ่ง ![]() จะได้ว่า
จะได้ว่า ![]()
โดยเขียน ![]() แทน
แทน ![]()
ตัวอย่าง
จงหาผลหารของจำนวนเชิงซ้อน ![]()
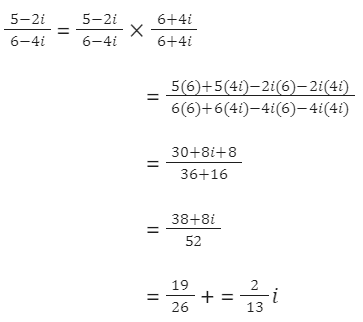
นี่เป็นเพียงเนื้อหาบางส่วนของจำนวนเชิงซ้อนเท่านั้น เนื่องจากเป็นเรื่องที่มีเนื้อหาค่อนข้างมาก ทำให้หลายคนอาจถอดใจไปกับบทเรียนนี้ได้ แต่พี่ ๆ เชื่อว่าหากน้อง ๆ ทบทวนพื้นฐานจนแม่น และฝึกทำโจทย์อย่างสม่ำเสมอ จำนวนเชิงซ้อนจะไม่ยากเกินความพยายามของเราแน่นอน
ส่วนใครที่กำลังมองหาที่ติวคณิตศาสตร์ หรือมีข้อสงสัยเพิ่มเติมก็มาปรึกษาพี่ TUTOR VIP ได้นะ พี่ ๆ ยินดีให้คำปรึกษาเสมอ
บทความต่อไป TUTOR VIP จะมาแนะนำอะไรอีกนั้น ฝากติดตามกันด้วยนะ
ด้วยความร่วมมือของ TUTOR-VIP X Clearnote Thailand







บทความล่าสุด
วิทยาศาสตร์
พลังงานไฟฟ้า เกิดขึ้นได้อย่างไร ปัจจุบันนี้มีวิธีผลิตกี่แบบ มาหาคำตอบกัน
วิทยาศาสตร์
ไฟฟ้ากระแสตรง(DC) และกระแสสลับ(AC) แตกต่างกันอย่างไร? มาไขคำตอบกัน
สังคมและประวัติศาสตร์
พระราชประวัติ และ พระราชกรณียกิจ สมเด็จพระนางเจ้าสิริกิติ์ ฯ